Hat Matrix Orthogonal Projection

Stack Exchange network consists of 177 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.
Hat matrix orthogonal projection. It is an exercise in the algebra of inner products to show that if P ρA B then PT ρB A no matter if P is orthogonal or not. I prove these results. Along the way I present the proo.
If a vector z z is orthogonal to every vector in a subspace W W of Rn R n then z z is said to be orthogonal to W W2. Eine Orthogonalprojektion von gr. 1 Find a basis v 1 v 2 v m for V.
Rather than derive a different projection matrix for each type of projection we can convert all projections to orthogonal projections with the default view volume This strategy allows us to use standard transformations in the pipeline and makes for efficient clipping Angel and Shreiner. A square matrix is called an orthogonal projection matrix if for a real matrix and respectively for a complex matrix where denotes the transpose of and denotes the adjoint or Hermitian transpose of. 2 Turn the basis v i into an orthonormal basis u i using the Gram-Schmidt algorithm.
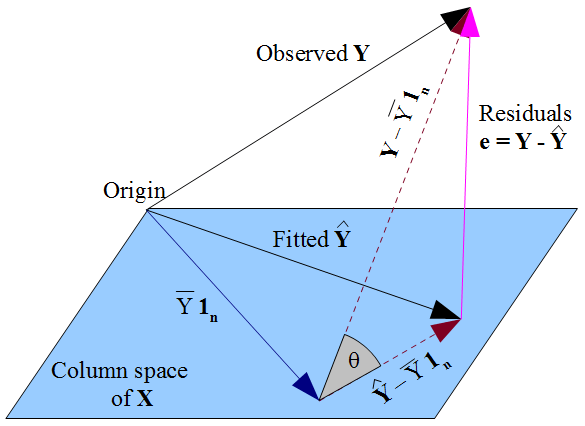
From the view point of statistical analysis we use two types of projections 1. 3 Your answer is P P u iuT i. We can show that both H and I H are orthogonal projections.
Note that this is an n n matrix we are multiplying a. These two conditions can be re-stated as follows. Its whole purpose is to convert xyz values to be between -1 and 1 so that the GPU knows whether points are inside our outside the screen and thus whether they need to be clipped or not.
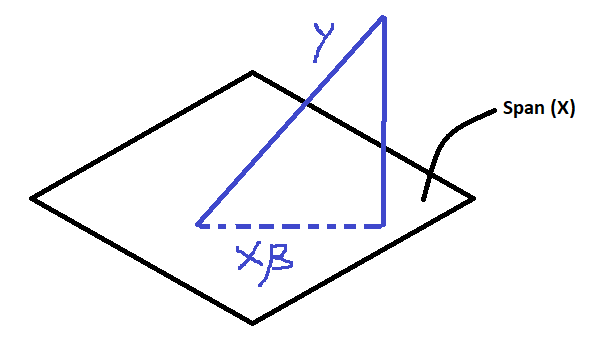
To nd the matrix of the orthogonal projection onto V the way we rst discussed takes three steps. 1A square matrix A is a projection if it is idempotent 2A projection A is orthogonal if it is also symmetric. Projection or Projection Matrix is a key tool or concept used many statistical methods projecting a vector into the span of few other vectors is a critical step in solving the linear regression or least square problem.